My approach to Riemann surfaces is via the Fenchel-Nielsen coordinates of the Teichmüller space associated to the unique geodesic pants decomposition of a surface. A pair of pants is homeomorphic to a sphere minus three open disks with Jordan curve boundaries. If a pair of pants is straightened to have closed geodesics as boundary components, it becomes a geodesic pair of pants. Closed geodesics drawn on a surface that separate it into geodesic pairs of pants gives a geodesic pants decomposition. The Fenchel-Nielsen coordinates on the Teichmüller space T(S) are associated to a geodesic pants decomposition of the surface S. Each closed geodesic in the decomposition is associated with its hyperbolic length, called the length coordinate. We also associate to it a twist, or the relative hyperbolic distance between feet of orthogeodesics drawn from the closed geodesic to the nearest closed geodesics on both sides. The lengths and twists constitute the Fenchel-Nielsen coordinates of a surface.

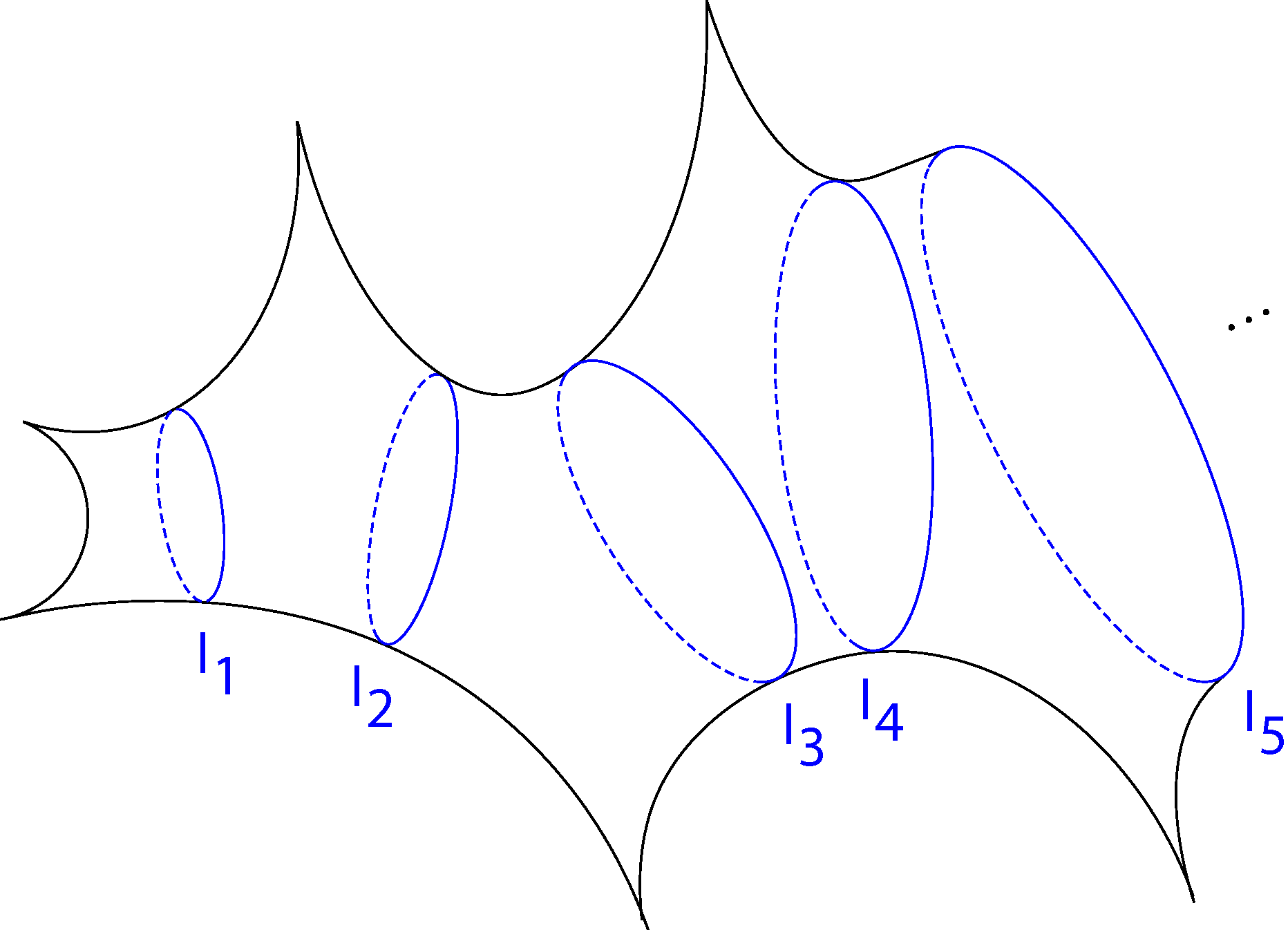
Figure 1: A half-twist tight flute surface X({ln, 1/2}).
Basmajian, Hakobyan, and Šarić in [BHS] extensively studied surfaces called tight flute surfaces. They constructed them in the following way. Start with a geodesic pair of pants with two punctures and a closed geodesic boundary. Attach geodesic pairs of pants with two closed geodesic boundaries and one puncture in an infinite chain. The result is a tight flute surface. They called the closed geodesics between pants, cuffs. Their lengths give the length coordinates {ln}, and their twists give the twist coordinates {tn}. When the twist of each cuff is one half, you get a half-twist tight flute surface (see Figure 1).
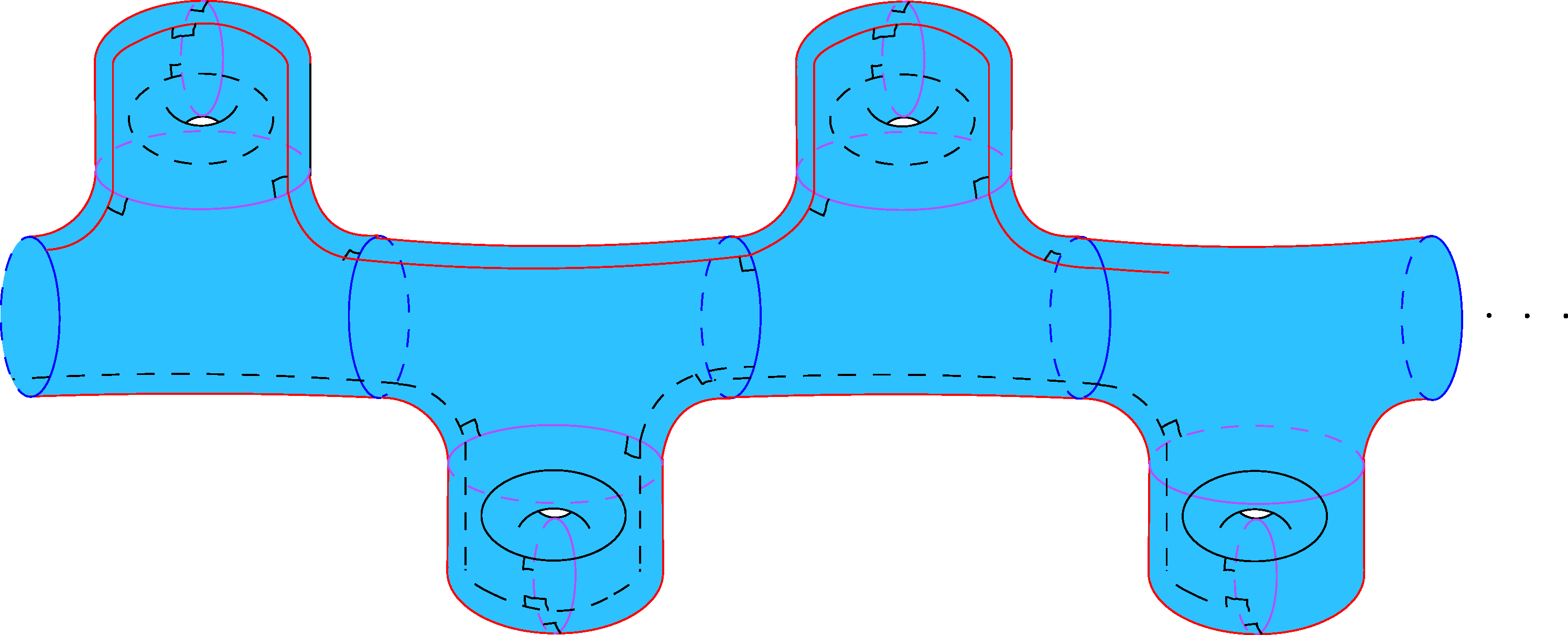
Figure 2: The tail of a half-twist Loch-Ness monster.
In [BHS], the parabolicity of surfaces called Loch-Ness monsters were determined using their Fenchel-Nielsen coordinates. They constructed a Loch-Ness monster by replacing each puncture of a tight flute surface with a closed geodesic, called ßn, and attaching a torus with a hole to each one. Šarić and I add an additional simple closed geodesic γn on each attached torus separated by ßn. We assume the lengths of ßn and γn are between two positive constants. When the twist of every cuff between pairs of pants is one half, the result is a a half-twist Loch-Ness monster. See Figure 2 for a picture of the tail of a half-twist Loch-Ness monster.

Figure 3: A surface with finitely many symmetric ends.
This led in [BHS] to the classification of parabolicity of a more general type of surface whose construction follows. Starting with a surface X0 with closed geodesic boundaries { δ1,...,δk}, attach to each δi a symmetric non-planar surface with one boundary a closed geodesic. The result is a surface with finitely many symmetric ends, or a symmetric end surface (see Figure 3). Each symmetric end is the tail of a Loch-Ness monster. We call the symmetric end surface minus the attached toruses its body.