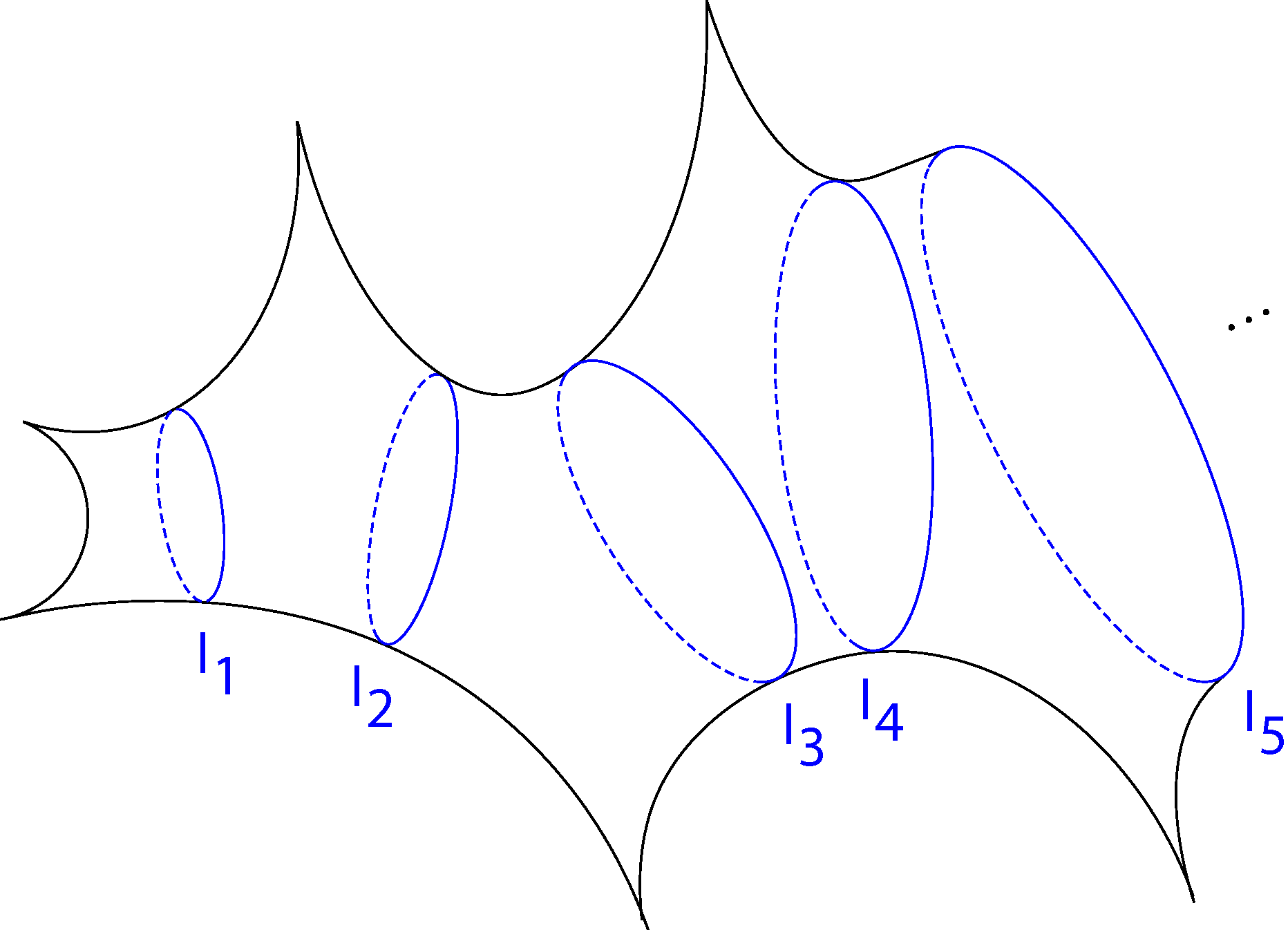
Figure 1. A half-twist tight flute surface.
Click the link below to see my joint paper with Dragomir Šarić.
Ergodicity of the geodesic flow on symmetric surface
The focus of my research is on hyperbolic geometry, Riemannian surfaces, and Teichmüller theory. In my thesis, I study conformally hyperbolic symmetric surfaces with infinitely generated fundamental groups.
My approach to Riemann surfaces is via the Fenchel-Nielsen coordinates of the Teichmüller space associated to the unique geodesic pants decomposition of a surface. A pair of pants is homeomorphic to a sphere minus three open disks with Jordan curve boundaries. If a pair of pants is straightened to have closed geodesics as boundary components, it becomes a geodesic pair of pants. Closed geodesics drawn on a surface that separate it into geodesic pairs of pants gives a geodesic pants decomposition. The Fenchel-Nielsen coordinates on the Teichmüller space T(S) are associated to a geodesic pants decomposition of the surface S. Each closed geodesic in the decomposition is associated with its hyperbolic length, called the length coordinate. We also associate to it a twist, or the relative hyperbolic distance between feet of orthogeodesics drawn from the closed geodesic to the nearest closed geodesics on both sides. The lengths and twists constitute the Fenchel-Nielsen coordinates of a surface.
Basmajian, Hakobyan, and Šarić considered a question concerning the classification of Riemann surfaces, called the type problem. They asked whether Riemann surfaces were of parabolic type, which means they do not support a Green's function. They point to various equivalent statements with parabolicity in function theory, dynamics, and geometry to highlight its importance. If the Riemann surface X is the quotient of the hyperbolic plane by a Fuchsian group, then X is parabolic if and only if the harmonic measure of the ideal boundary vanishes, or the geodesic flow on the unit tangent bundle of X is ergodic, or ΣγεΓe-dh(z,γ(z)) diverges where dh(.,.) is the hyperbolic distance in H and z in H.
The main goal of my work is to clearly state relationships between the hyperbolic geometry of particular Riemann surfaces of interest and their type. With sufficient conditions on the Fenchel-Nielsen coordinates of a surface, the joint work with D. Šarić guarantee that the surface is of parabolic type. We showed that parabolicity and having covering groups of the first kind are equivalent for certain hyperbolic surfaces of interest.
In order to show that surfaces have Fuchsian covering groups of the first kind, we showed that all escaping geodesic rays on surfaces have infinite length. This was done using the universal cover of either the front of a surface or part of its front. Our results have found equivalent statements of parabolicity for special symmetric surfaces. Some of this work is briefly described in the following two sections below.

Figure 1. A half-twist tight flute surface.
Basmajian, Hakobyan, and Šarić in [BHS] extensively studied surfaces called tight flute surfaces. They constructed them in the following way. Start with a geodesic pair of pants with two punctures and a closed geodesic boundary. Attach geodesic pairs of pants with two closed geodesic boundaries and one puncture in an infinite chain. The result is a tight flute surface. They called the closed geodesics between pants, cuffs. Their lengths give the length coordinates {ln}, and their twists give the twist coordinates {tn}. When the twist of each cuff is one half, you get a half-twist tight flute surface (see Figure 1).
In [BHS], Basmajian, Hakobyan, and Šarić showed for half-twist flute surfaces, Xf1/2, (1) Σn=1∞e-ln/4=∞ implies Xf1/2 is parabolic. If the length parameters are increasing and concave, the sum is infinite if and only if Xf1/2 is parabolic if and only if its covering group is of the first kind. With σn=ln - ln-1+...+(-1)n-1l1, if (2) Σn=1∞e-σn/2 < ∞, they showed Xf1/2 has covering group of the second kind.
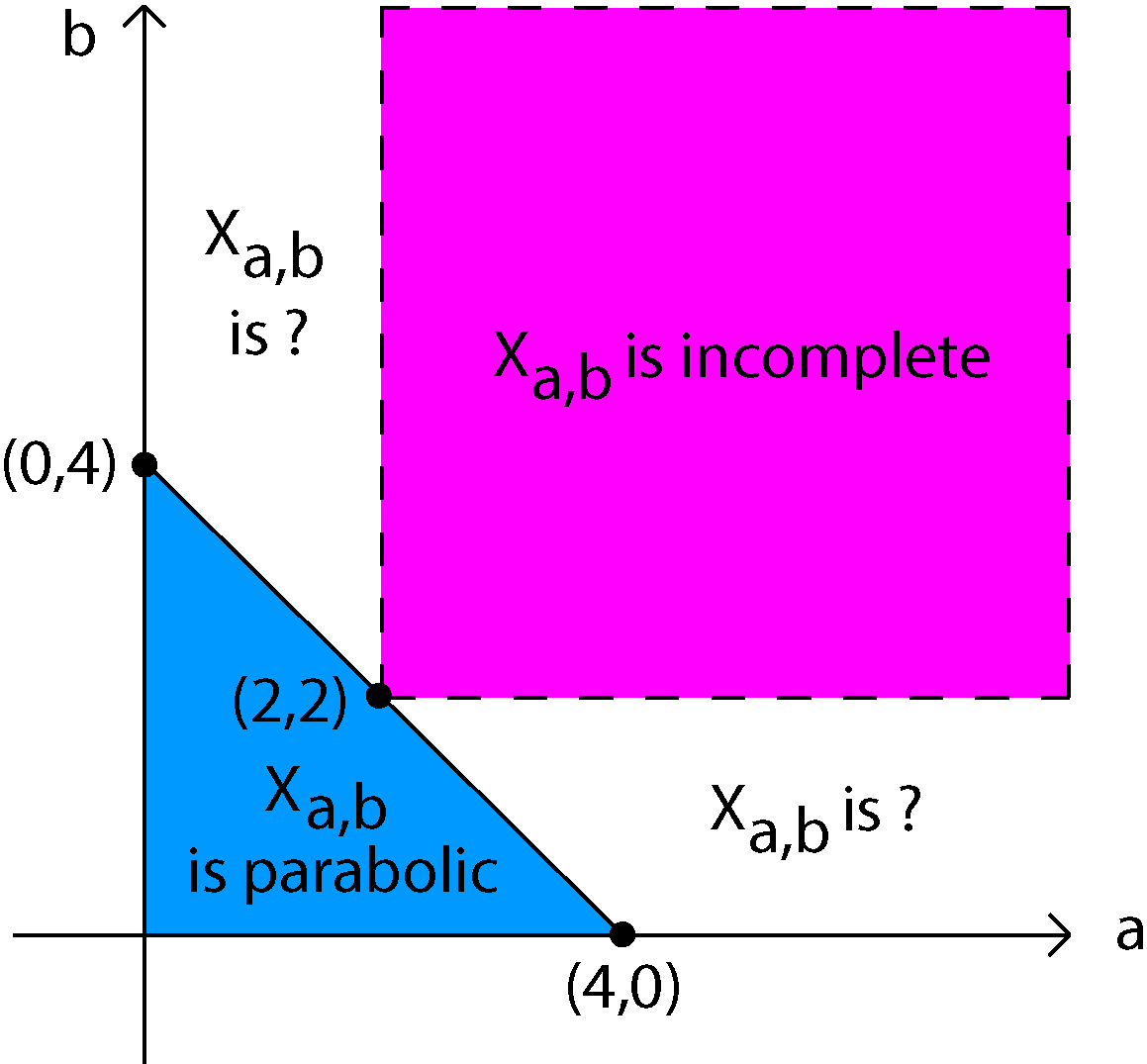
Figure 2. A two-parameter family of half twist flutes Xa,b where a and b are both positive.
Hakobyan created the Hakobyan Slice (see Figure 2), a two-parameter family of half-twist flutes $X_{a,b}$ with $a$ and $b$ positive that illustrates the relationships between conditions (1) and (2). The length parameters of $X_{a,b}$ are increasing, not concave, and defined by
l2n=aln(n+1)+bln(n) and l2n+1=(a+b)ln(n+1).
If a+b ≤ 4, then (1) is infinite and Xa,b is parabolic. However, if min{a,b} > 2, then (2) is finite and Xa,b is incomplete or has covering group of the second kind. It was an open question whether or not Xa,b without conditions (1) and (2) were parabolic or complete.
One of the primary goals of my thesis was to study the Xa,b in the Hakobyan slice such that neither condition (1) nor (2) is satisfied to find general statements that explained when half-twist tight flutes are parabolic. Šarić and I succeeded in this endeavor in our joint research, and found that for half-twist flute surfaces with increasing length parameters, its covering group is of the first kind if and only if Σn=1∞e-σn/2 = ∞ if and only if it is parabolic. This leads to the conclusion that Xa,b has Fuchsian covering group of the second kind if and only if min{a,b} > 2, and Xa,b is parabolic if and only if min{a,b} ≤ 2.
In [BHS], the parabolicity of surfaces called Loch-Ness monsters were determined using their Fenchel-Nielsen coordinates. They constructed a Loch-Ness monster by replacing each puncture of a tight flute surface with a closed geodesic, called βn, and attaching a torus with a hole to each one. Šarić and I add an additional simple closed geodesic γn on each attached torus separated by βn. We assume the lengths of βn and γn are between two positive constants.
This led in [BHS] to the classification of parabolicity of a more general type of surface whose construction follows. Starting with a surface X0 with closed geodesic boundaries { δ1,...,δk}, attach to each δi a symmetric non-planar surface with one boundary a closed geodesic. The result is a surface with finitely many symmetric ends, or a symmetric end surface. Each symmetric end is the tail of a Loch-Ness monster. We call the symmetric end surface minus the attached toruses its body.
Determining parabolicity of symmetric end surfaces was now attainable from the tools acquired in the joint research of Saric and I on half-twist flutes. It was found that if, in the body of each end, the cuffs have zero twists and their lengths {ln} are increasing, then Σn=1∞e-ln/2=∞ in each end if and only if the surface is parabolic. If the twists of the same cuffs are instead one half, then Σn=1∞e-σn/2 = ∞ in each end if and only if the symmetric end surface is parabolic.
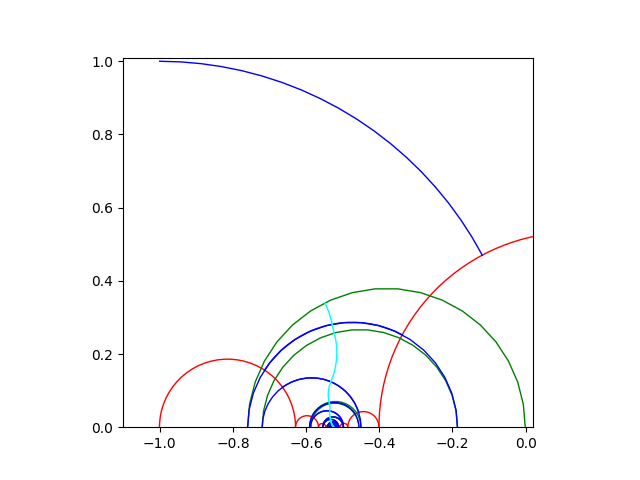
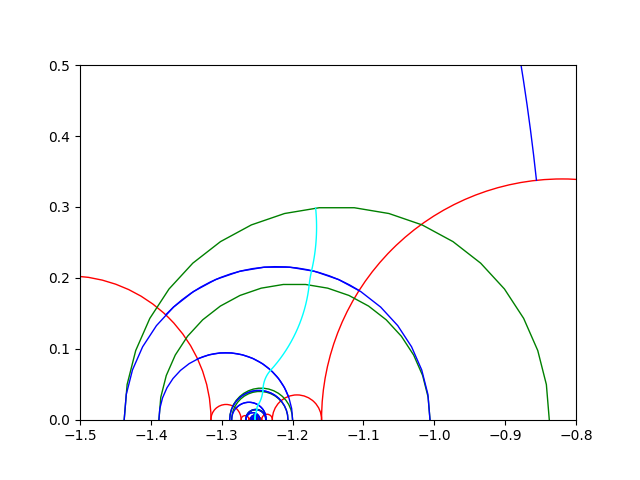
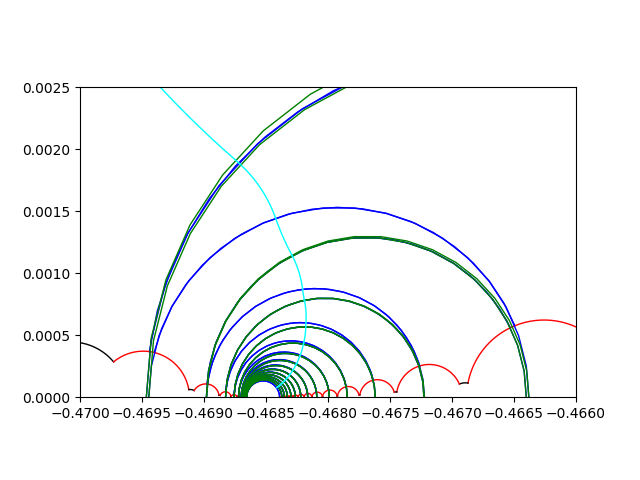
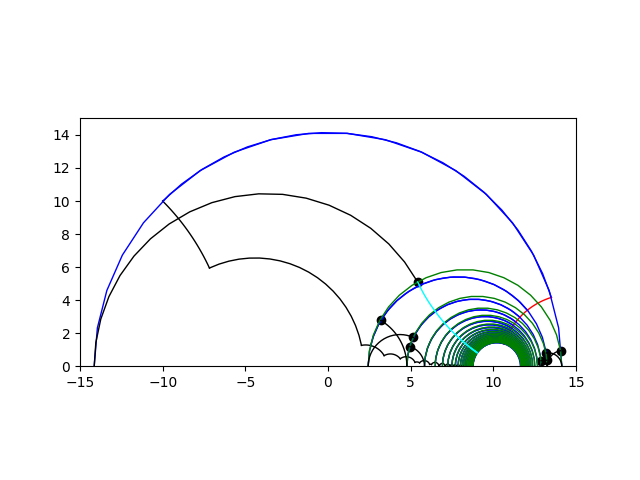
Figure 3. A concatenation of horocylic arcs drawn precisely from python coding for X4,1.
Šarić's work in [S] shows that when a concatenation of horocyclic arcs drawn on the surface is infinite length then lifts of the cuffs in the universal cover do not converge in D (see Figure 3). This results in all escaping geodesic rays on the surface being infinite length, or the surface being complete, or the covering group being of the first kind. Basmajian, Hakobyan, and Šarić found for a half-twist flute with increasing ln, if Σn=1∞e-σn/2 < ∞, where σn=ln - ln-1+...+(-1)n-1l1, then a concatenation of summits of Saccheri quadrilaterals made on the surface is finite length. That means the flute is incomplete.
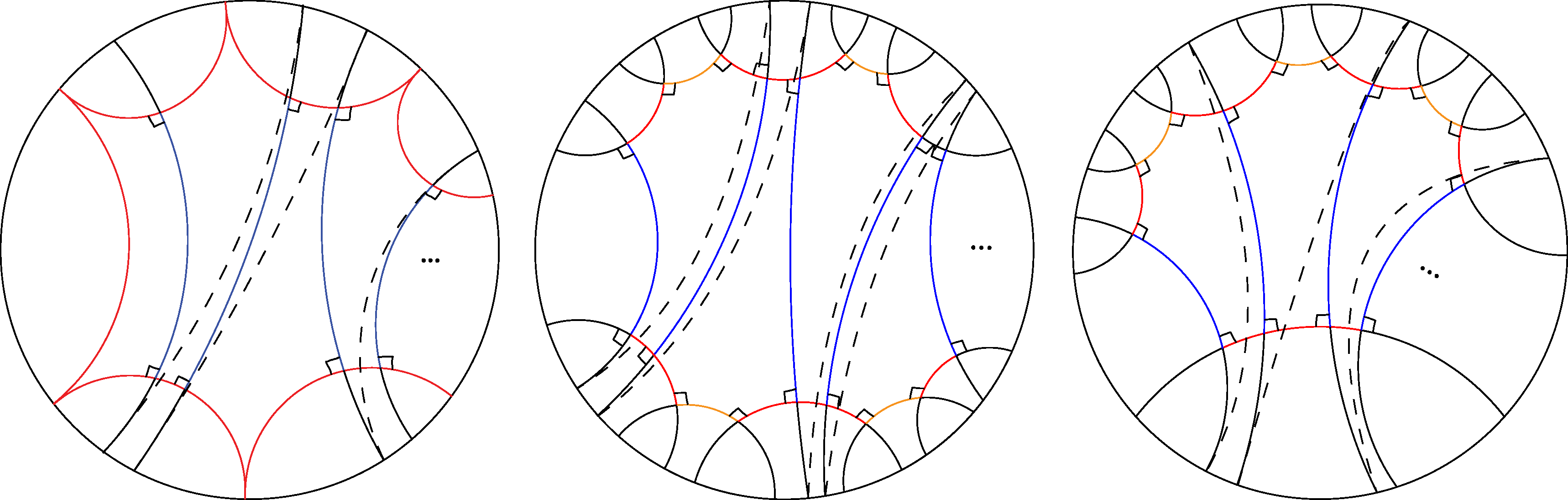
With python programming, I drew precise pictures of the universal covers of the fronts of half-twist flutes (see Figure 3), and of the fronts of the bodies of zero and half-twist Loch-Ness monsters. All that was needed to get the desired results of our research were the fronts of these surfaces due to their symmetry. The universal covers showed horocyclic paths drawn on the pants decompositions of these surfaces, as well as concatenations of summits of Saccheri quadrilaterals. Their lengths were needed to use the results of Basmajian, Hakobyan, and Šarić. Calculations in the python programs I created informed the results of the joint work with D. Šarić.

How to build tight flutes and Loch-Ness monsters Universal covers of half-twist flutes Universal covers of half-twist Loch-Ness monsters Universal covers of zero-twist Loch-Ness monsters