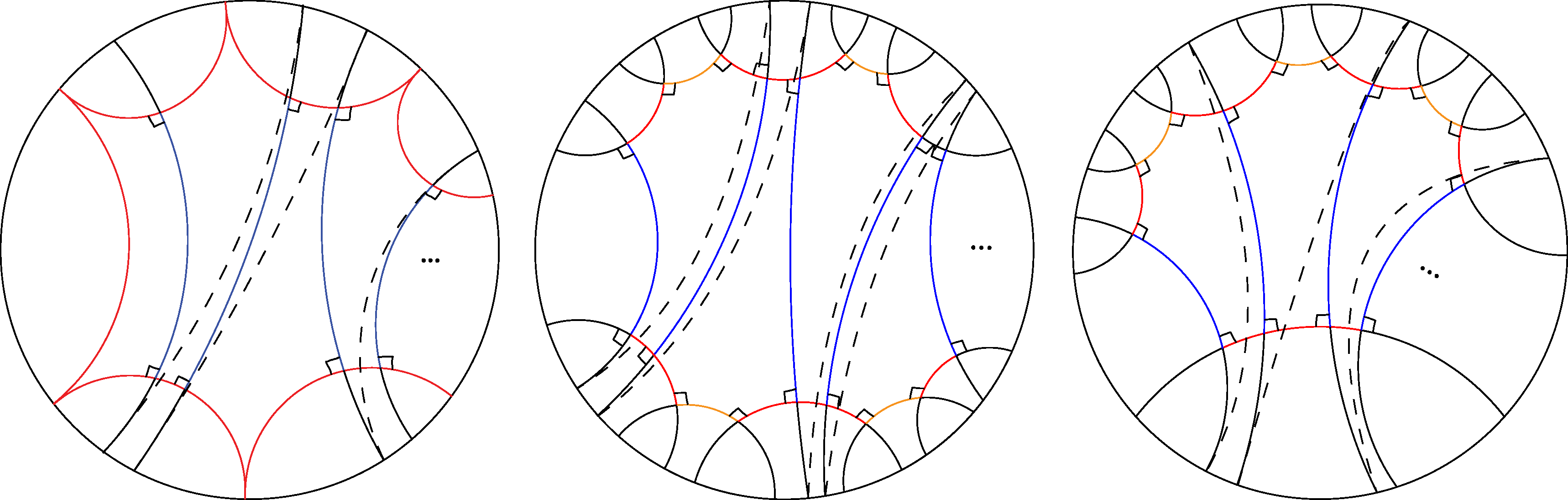
Figure 1. The Cantor tree surface with a geodesic pants decomposition.
Click the link below to see my individually authored paper.
Non-ergodicity of the geodesic flow on Cantor tree surface
A Riemann surface equipped with its conformal hyperbolic metric is parabolic if and only if the geodesic flow on its unit tangent bundle is ergodic. Let X be a Cantor tree or a blooming Cantor tree Riemann surface. Fix a geodesic pants decomposition of X and call the boundary geodesics in the decomposition cuffs. Basmajian, Hakobyan, and Šarić proved that if the lengths of cuffs are rapidly converging to zero, then X is parabolic. More recently, Šarić proved a slightly slower convergence of lengths of cuffs to zero implies X is not parabolic. In the paper, we interpolate between the two rates of convergence of the cuffs to zero and find that these surfaces are not parabolic, thus completing the picture.
Figure 1. The Cantor tree surface with a geodesic pants decomposition.
A Cantor tree Riemann surface XC is conformal to the complement of a Cantor set in the Riemann sphere. Equivalently, XC is constructed by isometrically gluing countably many geodesic pairs of pants along their boundary geodesics (called cuffs) to form the ``shape'' of the dyadic tree (see Figure 1). In addition to the lengths of its cuffs, the Cantor tree Riemann surface XC is determined by the twists along the cuffs.
The cuffs of XC are grouped in the levels based on the level in the dyadic tree. At level zero, we have a single cuff, which is at the top of XC in Figure 1. At level one, we have four cuffs, and at level n ≥ 1, we have 2n+1 cuffs. Denote by {αnj}j=12n+1 the level n cuffs from left to right in Figure 1.
McMullen [McMullen] proved if there is a C > 0 such that 1/C ≤ l(αnj) ≤ C then X is not parabolic. This is a consequence of the fact that the Brownian motion has many directions to escape to infinity when the ideal boundary is large, in our case the Cantor set, and the cuffs (the openings) are not short.
| In the case when the cuffs are short Basmajian, Hakobyan and Šarić [BHS] proved XC is not parabolic if there is C > 0 such that l(αnj) ≤ C | n 2n |
, where l(.) is the hyperbolic length in X. |
More recently, Šarić[S, Theorem 8.3] proved that if
| l( αnj)= | nr 2n |
The remaining case to consider is whether XC is parabolic or not for $1 < r ≤ 2. We show the following.
| Theorem 1.1. Let XC be the Cantor tree surface as depicted in Figure 1 and l(αnj) for 1 ≤ j ≤ 2n+1 the cuffs at the level n. The cuff lengths are decreasing along each end. Then XC is not parabolic if there is an r > 1 such that |
| C1 | nr 2n | ≤ l(αnj) ≤ | C2 n2 |
Figure 2. The blooming Cantor tree surface with a geodesic pants decomposition.
Even for r > 2, the scope of our theorem is slightly more general than [S, Theorem 8.3] because we allow the lengths of the cuffs to vary with the given lower bound. We also extend our result to surfaces with infinite genus and a Cantor set of ends, called the blooming Cantor tree surfaces X̃C (see Figure 2). To construct the blooming Cantor tree from the Cantor tree, attach a geodesic surface of genus at most C and two boundaries, or do not, to each level n boundary αnj (see that α01=α02=α0) and redefine αnj to be the boundary of the attached surface further away from α0 for n ≥ 0 and for 1 ≤ j ≤ 2n+1 and for a universal constant C>0. We can add 2n+1 surfaces at the level n of genus at most C for n ≥ 0. Assume the lengths of cuffs along each attached geodesic surface are decreasing.
| C1 | nr 2n | ≤ l(αnj) ≤ | C2 n2 |