CV MICHAEL PANDAZIS

PERSONAL INFORMATION

Name: Michael Pandazis

Email address: michaelantonypandazis@gmail.com

PROFILE

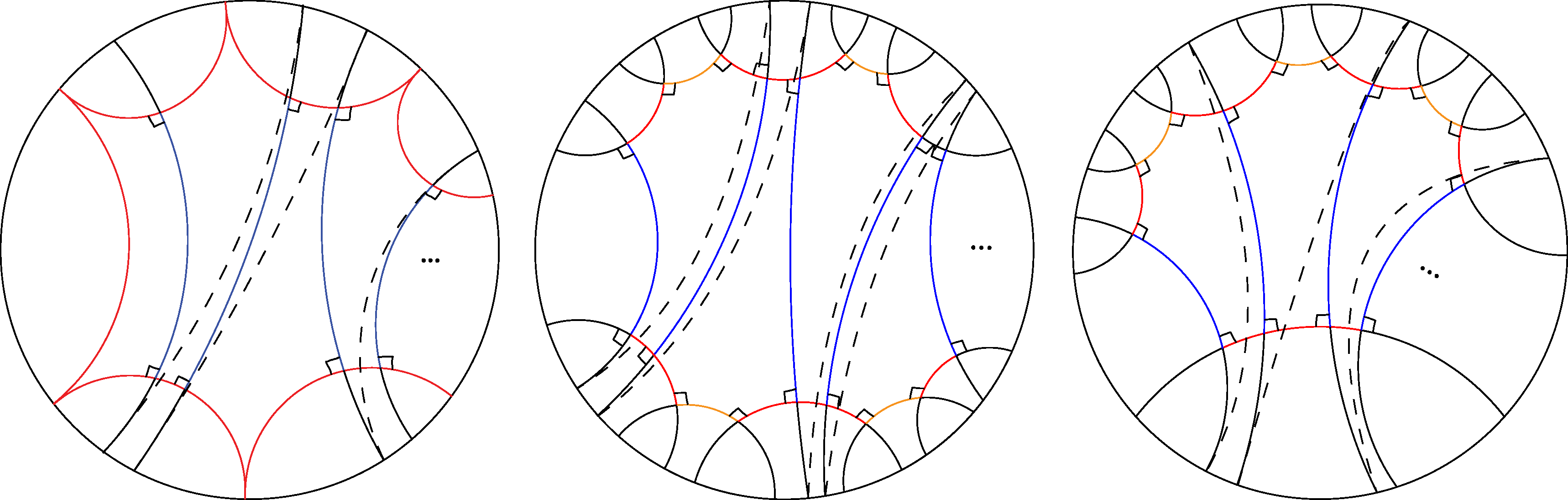
I graduated from the CUNY Graduate Center with a Math Ph.D. in June of 2024. Broadly speaking, my research falls between the areas of Geometric Function Theory and Low-Dimensional Topology. In my thesis I study the hyperbolic geometry and quasiconformal deformations of infinite Riemann surfaces; in particular, I am considering sufficient conditions on the Fenchel-Nielsen coordinates that result in infinite Riemann surfaces having ergodic geodesic flow. A joint paper with my advisor Dragomir S ̌aric ́ on this topic, entitled Ergodicity of the geodesic flow on symmetric surfaces, is published in Transactions of the American Mathematical Society. This paper was on flute surfaces and surfaces with symmetry and finitely many ends. Moreover, a single-authored paper was accepted for publication by Proceedings of the American Mathematical Society, called “Non-ergodicity of the geodesic flow on a special class of Cantor tree surfaces,” proving the non-parabolicity of blooming Cantor tree surfaces with length parameters between two rates of convergence to zero. It is available as a preprint on Arxiv, arXiv:2310.10415. I am working on a joint paper with Hrant Hakobyan and my advisor Dragomir S ̌aric ́ that proves there are parabolic zero and half-twist flute surfaces with cuff lengths that increase arbitrarily fast. The joint paper is also available as a preprint per request. I have ample teaching experience as an adjunct lecturer in the mathematics department at CUNY Queens College for the last 13 years and from teaching high school students at CUNY Baruch College. My long-term goal is to be a tenured professor. I am energetic, motivated, and determined to excel in all my endeavors.

RESEARCH INTERESTS

• Hyperbolic Geometry
• Quasiconformal Teichmuller Theory
• Complex Analysis

EDUCATION

• CUNY Graduate Center, PhD in Philosophy (Mathematics) - June,  2024.
• CUNY Graduate Center, Masters in Philosophy (Mathematics) - January, 2022  
• Queens College, Masters of Arts, Pure Mathematics - May, 2012
• Queens College, Bachelors of Arts, Mathematics - May, 2010
• Bronx High School of Science, Regents Diploma - May, 2004

PROFESSIONAL EXPERIENCE

• Adjunct Lecturer Queens College, CUNY September, 2010 – Present
• Tutor REF CUNY September 2021 – Present
• Tutor in Mathematics Lab Queens College, CUNY February, 2010 – 2013

RESEARCH EXPERIENCE

• “Parabolic and Non-Parabolic Surfaces with Small or Large End Spaces via Fenchel-Nielsen Parameters” is my completed thesis. Professor Dragomir S ̌aric ́ is my advisor, and my defense committee also includes Professor Ara Basmajian and Professor Enrique Pujals.
• “Ergodicity of the geodesic flow on symmetric surfaces” is a joint paper with Professor Dragomir Šarić that is published by and appears in Transactions of the American Mathematical Society 376 (2023), no. 10, 7013-7043.
• “Non-ergodicity of the geodesic flow on a special class of Cantor tree surfaces” is single-authored and accepted for publication by Proceedings of the American Mathematical Society. It is available as a preprint on Arxiv, arXiv:2310.10415..
• "Parabolicity through twisting” is a joint paper with Hrant Hakobyan and Dragomir Šarić that is also in preparation. It is available as a preprint per request. 

PRESENTATIONS

•   Gave a presentation on “Ergodicity of the geodesic flow on symmetric surfaces” for the XIII Symposium “Mathematics and Applications” online, organized by the faculty of mathematics at the University of Belgrade and the Serbian Mathematical Society on Dec 2nd, 2023.
• Gave a presentation at CUNY Bronx Community College at the math department seminar on “Ergodicity of the geodesic flow on symmetric surfaces,” on Oct 31st, 2023.
• Presentation at the AMS Special Session on Geometry of Groups and Spaces at the University of Buffalo on “Ergodicity of the geodesic flow on symmetric surfaces,” in 2023. Was awarded a travel award from the Umesh & Shailaja Nagarkatte Fellowship Fund by the CUNY Graduate Center to help with the costs of presenting the paper and attending the conference. The AMS also awarded me with travel support for my attendance at the AMS Sectional Meeting.
• Gave a presentation on “Ergodicity of the geodesic flow on symmetric surfaces” at Kansas State University at an Analysis Seminar, in 2023.
• Speaker at the Hyperbolic geometry seminar at the CUNY Graduate Center on “Ergodicity of the geodesic flow on symmetric surfaces,” in 2023. 
• Chalk talk on “Ergodicity of the geodesic flow on symmetric surfaces” to Queens College professors in 2022. 

SKILLS

• Programming Languages: Python, Latex, C++, and HTML
• Programmed precise models of the universal covers of fronts of half-twist tight flute surfaces, and parts of the fronts of zero and half-twist Loch-Ness monsters to study their completeness and parabolicity using Python programming in PyCharm. Also used Python programming to calculate values of shears and to draw horocyclic arcs.
• Software: PyCharm, Illustrator, Microsoft Word, Dreamweaver, Gummi, Excel, PowerPoint, Mathematica